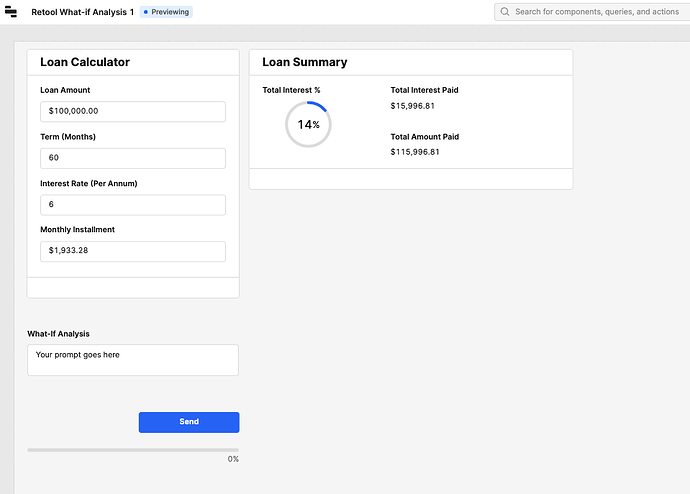
Consider a scenario where a business takes out a loan of $100,000, aiming to repay it over five years with a 6% annual interest rate. Utilizing Retool, calculating the monthly repayment amount is straightforward, yielding a figure of $1,933. This calculation, while useful, represents only a fraction of the financial insights businesses require today.
The question then arises: what if our repayment capabilities are more robust than initially projected? For instance, if a business can afford a monthly payment of $2,500, how would this affect the total loan amount it could feasibly borrow? This reverse calculation, although less conventional, is crucial for businesses seeking to maximize their investment strategies and tailor their financial commitments to their actual repayment capacity.
This scenario underscores the necessity for a more flexible tool that can perform both traditional and reverse financial calculations. By integrating AI with Retool, we can unlock this capability, empowering users to conduct comprehensive sensitivity analyses. This approach not only enhances Retool's existing functionalities but also provides users with deeper insights into their financial decisions, enabling more informed strategic planning.
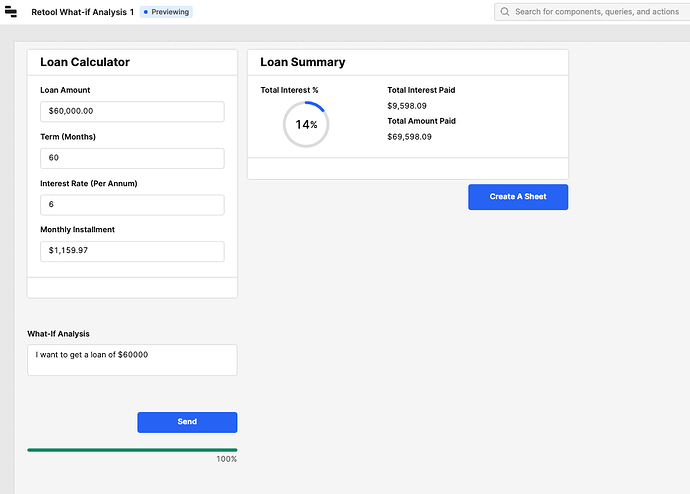
Let's take this example where we are looking for a loan of $60000 to be paid in 5 years.
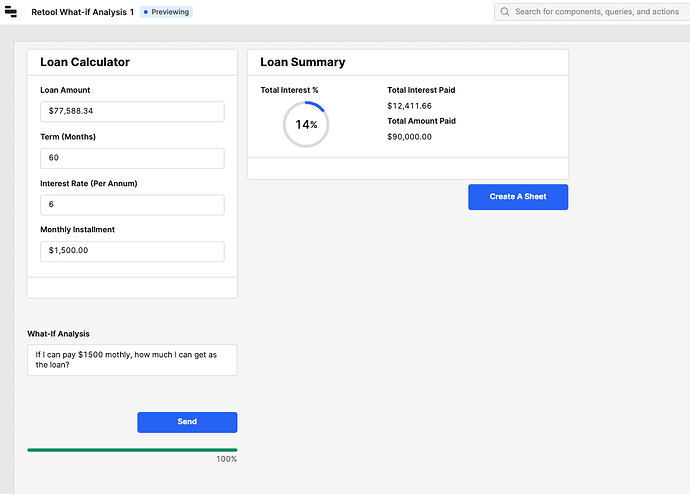
According to the calculations, we have to pay $1,159.97 per month. Now let's ask the question, what-if I can pay $1500 a month? we'll need to reverse-engineer the loan calculation to determine the maximum loan amount you could afford under these conditions.
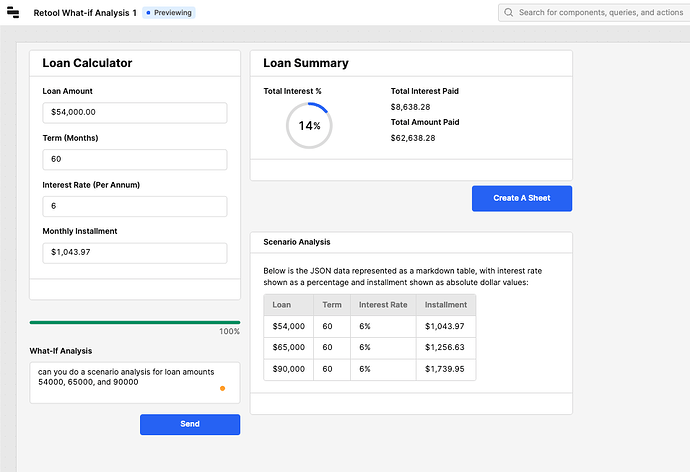
You can see in the above image how I got AI to come to our help to reverse engineer the calculation to show the loan we can go for. Take a look at the following video to get an idea of how it works. I even got it to produce a Google Sheet in this process.
Video demo of Sensitivity Analysis in Action
How can we use Sensitivity Analysis in our day-to-day work?
Sensitivity analysis is a powerful tool that can be applied in various day-to-day work scenarios across different industries and job functions. It involves changing one or more input variables in a given model to see how those changes affect the output. This technique helps in understanding how sensitive a result is to changes in input values, aiding in decision-making, risk management, and strategic planning. Here are some practical ways sensitivity analysis can be used in everyday work:
1. Financial Planning and Analysis
- Budgeting: Sensitivity analysis allows financial analysts to test how changes in sales volume, costs, or pricing affect profitability.
- Investment Decisions: By varying interest rates, market conditions, or investment amounts, investors can understand potential returns and risks.
2. Project Management
- Risk Assessment: Project managers can use sensitivity analysis to identify which variables (e.g., project duration, costs, resource availability) most impact project outcomes, helping to prioritize risk mitigation strategies.
- Resource Allocation: It helps in determining how changes in resource allocation affect project timelines and costs.
3. Marketing and Sales
- Pricing Strategies: Sensitivity analysis can help determine how changes in price affect demand and revenue.
- Market Analysis: By varying factors such as market size, growth rate, and competitor actions, companies can better prepare for different scenarios.
4. Product Development
- Cost Analysis: Identifying which components or processes most significantly impact the overall cost of production to focus cost reduction efforts.
- Performance Optimization: Understanding how different design changes affect product performance and user satisfaction.
5. Supply Chain Management
- Inventory Levels: Determining how changes in demand or supply lead times affect inventory requirements and costs.
- Supplier Risk: Analyzing the impact of supplier reliability and cost fluctuations on production schedules and costs.
6. Strategic Planning
- Scenario Planning: Sensitivity analysis supports the creation of various future scenarios (e.g., economic downturn, technological change) to strategize effectively.
- Decision Making: It provides a quantitative basis for choosing between different strategic options by assessing their potential impacts under various conditions.
Implementation in Tools Like Retool
Incorporating sensitivity analysis into tools like Retool can significantly enhance their utility by allowing users to create interactive applications that dynamically respond to changes in input variables. This can make complex analyses more accessible and actionable for decision-makers across the organization.
By understanding the impact of variable changes, businesses can make more informed decisions, allocate resources more efficiently, and better prepare for future uncertainties. Sensitivity analysis, therefore, is not just a theoretical exercise but a practical tool that can provide valuable insights in day-to-day work.
Next Steps
My next challenge is indeed a fascinating application of AI and Retool integration, showcasing the potential for advanced analytics in business decision-making. Linear Programming (LP) is a mathematical method used to find the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Your goal to determine the optimal product mix that maximizes profit is a classic LP problem, often referred to as the "mix" or "blending" problem.
Steps to Approach the Challenge:
- Define the Problem Clearly: Begin by identifying the constraints (e.g., resource limitations, capacity, demand) and the objective function (e.g., maximize profit). Each product will have associated costs, selling prices, and potentially, constraints on how much can be produced or sold.
- Gather Data: Collect all relevant data, including the profit margin for each product, available resources (like labor hours, materials), and any constraints on production or sales.
- Set Up the Model: Your LP model will include:Objective Function: This is usually profit maximization, defined as the sum of the profit per unit of each product times the number of units sold.Constraints: These include resource limitations (e.g., material or labor hours available), demand constraints, and any other limitations specific to your scenario.
- Solve Using AI and Retool: Although Retool and AI platforms like OpenAI are not traditional tools for solving LP problems, you can creatively leverage them. For instance, you could use OpenAI to generate the LP formulation based on your inputs and then utilize Retool to interactively adjust parameters and visualize solutions. The AI can assist in identifying constraints and setting up the objective function based on natural language inputs.
- Interpret and Apply Results: Once you have the solution, interpret the results to understand the optimal product mix. This step might involve analyzing how changing certain parameters affects the solution, which is a form of sensitivity analysis.
Integrating AI and Retool:
- Using AI for Problem Formulation: You could prompt the AI to help formulate the LP problem based on your business scenario. This includes generating the objective function and identifying constraints based on natural language descriptions of the business case.
- Retool as an Interactive Solver: Although Retool doesn't natively solve LP problems, you can integrate it with APIs or custom code that does. You can create a Retool application that accepts input parameters (like product prices, resource availability, and constraints), sends this data to a solver (which could be an API that performs LP calculations), and then displays the results in an interactive and user-friendly manner.
- Visualization and Sensitivity Analysis: Use Retool to build dashboards that visualize the outcomes of different product mixes and perform sensitivity analysis. This can help in understanding how changes in input variables (like cost prices, demand, etc.) impact the optimal solution.
This approach requires a blend of mathematical understanding, programming skills, and creative use of available tools. It's a great example of how modern technologies can be combined to tackle complex business problems that traditionally rely on specialized software.